嗨！同学们好！研粒考研教研室老师每周会根据学生答疑记录，汇总出大家备考中遇到的高频重难点问题。希望能够帮助到备考中有困惑的你，一起看看！

英语

1. We need to create a vision for public health where all of society works together to get healthy and live longer. 这句话中where是什么从句？

答：where引导定语从句，一般来说修饰前面表示地点的具体名词句，但是，该句中where为定语从句，修饰抽象名词vision,where在从句中充当状语。

复习建议：这个知识点，我们后期语法课程会讲到，暂时先记住即可，之后通过长难句进行多加练习即可。

2.倍数的表达

答：英语中，倍数的表达有三种：

1. 倍数 + as + 形容词或副词的原级 + as + 其他 

2. 倍数 + 形容词(或副词)的比较级 + than + 其他

3. 倍数 + the size / height / length / width. etc. + of + 其他

4. 比如dozens of

复习建议：这个知识点，可能在写作中需要大家具体掌握，同学们需要掌握这三种中的任一一种，重点掌握倍数和固定表达的顺序即可。

政治

1.矛盾双方相互转化推动事物的发展？

答：这个提法并不正确。矛盾是事物发展的动力，但是矛盾既包含着斗争性也包含着同一性，是有条件的相对的同一性和无条件的绝对的斗争性相结合,构成了事物的矛盾运动,推动着事物的发展。

复习建议：这个提法往往就是把概念杂糅在一起，然后看起来很对的样子，其实质是分清概念，里面包含几种意思，要理顺，才能辨别。

2.联系的普遍性

答：关于联系的普遍性有三层含义，很好理解，这个普遍性还要知道它的一层意思，是指任何事物不能孤立存在，都是同其他事物处于一定的联系之中。

复习建议：关于它里面包含的这层含义更重要，经常会作为考察，要能理解题目中的问法。

数学

1.

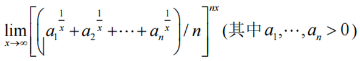
答：此极限为幂指函数型，应先用e抬底，转化为∞*0型。然后将x放在分母的位置变为1/x，换元t=1/x后，用洛必达法则。其中需要注意指数和对数函数的变形。

复习建议：幂指函数型抬底应该形成肌肉记忆。

除此之外，求极限的基本步骤要记得：先定型，后化简，最后定法，定型了自然会有相应思路。

2.ρ=acosθ，ρ=a(cosθ+sinθ)如何画图？

答：已知有x=ρcosθ,y=ρsinθ，故x^2+y^2=ρ^2，对ρ=acosθ两边同乘ρ，得ρ^2=aρcosθ，也即：x^2+y^2=ax，为偏心圆。

ρ=a(cosθ+sinθ)处理方式相同。对于极坐标方程来说，直接在极坐标中画图存在困难且容易出错，此时我们应尽量转化为直角坐标方程，在直角坐标系中画图。

两种方程只是表达形式不同，图像是完全一致的。

复习建议：除了会将极坐标方程转化为直角坐标方程外，常见的无法转化的极坐标方程也应熟记。例如：心形线、星形线、摆线、对数螺线、伯努利双纽线。